Pertidaksamaan Nilai Mutlak Linear Satu Variabel
Thursday, July 18, 2019
Add Comment
Hii Sobat SM4TIK!!! Jumpa lagi bersama dalam sm4tik.blogspot.com. Pada artikel sebelumnya sudah kita bahas mengenai Persamaan Nilai Mutlak Satu Variabel. Selanjutnya, kali ini kita akan membahas tentang Pertidaksamaan Nilai Mutlak Satu Variabel. Pada kesempatan ini akan kita ulas secara singkat, padat dan jelas terkait materi tersebut. Mari disimak!!!
Pertidaksamaan Nilai Mutlak Linear Satu Variabel
Menyelesaikan pertidaksamaan nilai mutlak caranya hampir sama dengan persamaan nilai mutlak. hanya saja berbeda sedikit pada tanda ketidaksamaannya. Langkah-langkah selanjutnya seperti menyelesaikan pertidaksamaan linear atau kuadrat satu variabel .
Pertidaksamaan mutlak dapat digambarkan sebagai berikut.
Apabila fungsi di dalam nilai mutlak berbentuk ax + b maka pertidaksamaan nilai mutlak dapat diselesaikan seperti berikut.
Lebih jelasnya perhatikan contoh berikut ini.
Contoh
Tentukan himpunan penyelesaian dari Pertidaksamaan nilai mutlak berikut ini.
Jawaban:
1. Cara menyelesaikan pertidaksamaan mutlak ini sebagai berikut.
-9 < x+7 < 9
-9 - 7 < x < 9 - 7
-16 < x < 2
Jadi, himpunan penyelesaiannya adalah { x/ -16 < x < 2}
2. Cara menyelesaikan pertidaksamaan mutlak ini dibagi menjadi dua bagian.
(*) 2x - 1 >= 7
2x >= 7 + 1
2x >= 8
x >= 4
(**) 2x - 1 <= -7
2x <= -7 + 1
2x <= -6
x <= -3
Jadi, himpunan penyelesaiannya adalah { x/ x <= -3 atau x >= 4}
3. Kalau dalam bentuk soal ini, langkah menyelesaikan pertidaksamaannya dengan mengkuadratkan kedua ruas.
perhatikan proses berikut ini.
(x + 3)2 <= (2x – 3)2
(x + 3)2 - (2x – 3)2 <= 0
(x + 3 + 2x – 3) - (x + 3 – 2x + 3) <= 0 (ingat: a2 – b2 = (a+b)(a-b))
x (6 - x) <=0
Pembuat nol adalah x = 0 dan x = 6
Mari selidiki menggunakan garis bilangan
Oleh karena batasnya <= 0, maka penyelesaiannya adalah x <=0 atau x >=6.
Jadi, himpunan penyelesaiannya adalah {x/ x <= 0 atau x >= 6}.
Mari selidiki menggunakan garis bilangan
Oleh karena batasnya <= 0, maka penyelesaiannya adalah x <=0 atau x >=6.
Jadi, himpunan penyelesaiannya adalah {x/ x <= 0 atau x >= 6}.
4. Menyelesaikan pertidaksamaan nilai mutlak seperti ini lebih mudah menggunakan cara menjabarkan definisi. Prinsipnya adalah batasan-batasan pada fungsi nilai mutlaknya.
Perhatikan pada 3x + 1 dan 2x + 4.
Dari batasan-batasan itu maka dapat diperoleh batasan-batasan nilai penyelesaian seperti pada garis bilangan di bawah ini.
Dengan garis bilangan tersebut maka di pengerjaannya dibagi menjadi 3 bagian daerah penyelesaian.
1. Untuk batasan x >= -1/3 ......(1)
(3x + 1) - (2x + 4) < 10
3x + 1 - 2x- 4 < 10
x- 3 < 10
x < 13 .......(2)
Dari (1) dan (2) diperoleh irisan penyelesaian -1/3 <= x < 13
2. Untuk batasan -2<= x < -1/3 ......(1)
-(3x + 1) - (2x + 4) < 10
-3x - 1 - 2x - 4 < 10
-5x - 5 < 10
-5x < 15
-x < 3
x > 3 .......(2)
Dari (1) dan (2) tidak diperoleh irisan penyelesaian atau tidak ada penyelesaian.
3. Untuk batasan x < -2 ......(1)
-(3x + 1) + (2x + 4) < 10
-3x - 1 + 2x + 4 < 10
-x + 3 < 10
-x < 7
x > -7 .......(2)
Dari (1) dan (2) diperoleh irisan penyelesaian -7 < x < -2.
Demikian ulasan singkat materi Pertidaksamaan Nilai Mutlak Linear Satu Variabel. Semoga ulasan materi pada artikel ini bisa bermanfaat untuk menambah wawasan dalam memahami dan mempelajari matematika khususnya materi Pertidaksamaan Nilai Mutlak Linear Satu Variabel. Sampai jumpa lagi di artikel lainnya di sm4tik.blogspot.com.






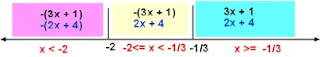








0 Response to "Pertidaksamaan Nilai Mutlak Linear Satu Variabel"
Post a Comment